第9日目

1. 講義資料
2. 特性インピーダンス, 伝搬定数
3. 定在波, 各種線路, まとめ
   • 入射波のイメージ
   • 反射波のイメージ
   • 定在波のイメージ(入射波と反射波の重ね合わせ)
   • 無損失線路での定在波と定在波比
4. 演習の解説

特性インピーダンス, 伝搬定数

定在波, 各種線路, まとめ

入射波

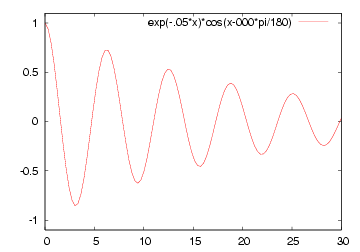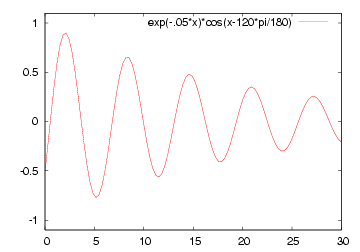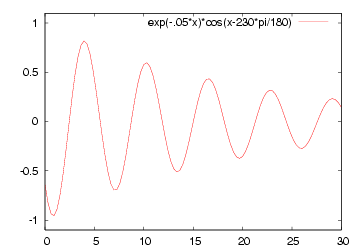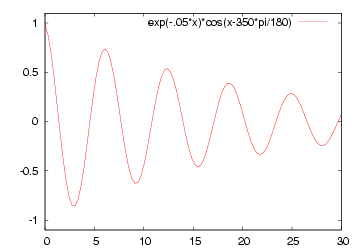
減衰なし	減衰あり
Acos(βx - ωt)	Ae-αx cos(βx - ωt)

反射波

減衰なし	減衰あり
Bcos(βx + ωt)	Beαx cos(βx + ωt))

定在波(入射波と反射波の重ね合わせ)

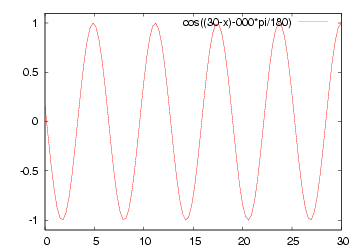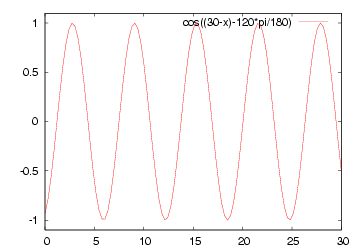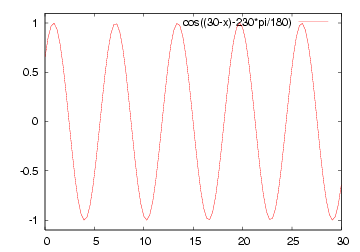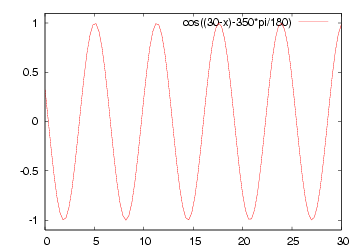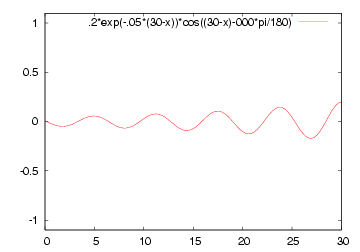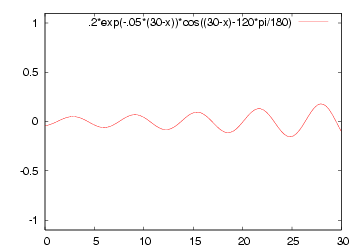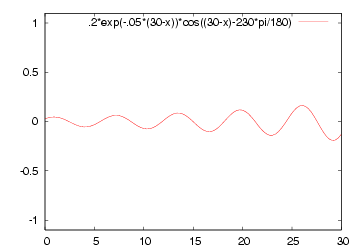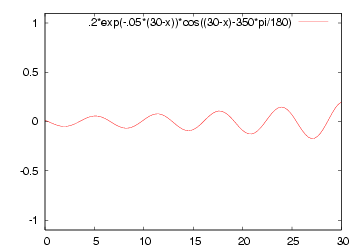減衰のない場合の例	減衰のある場合の例
A cos(βx - ωt) + A cos(βx + ωt)	Ae-αx cos(βx - ωt) + B e+αx cos(βx + ωt)

無損失線路での定在波と定在波比

1. 電圧定在波比 : ρ=1, インピーダンスマッチング(整合, 定在波なし, 各部で電圧振幅が等しい)

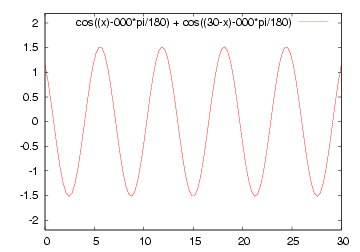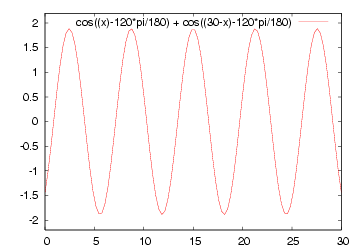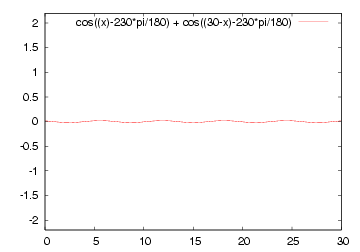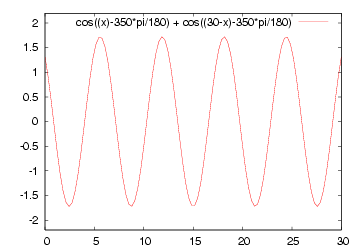   無限長線路 や Zoで終端された線路 の各部電圧波形

2. 電圧定在波比: ρ=2, 腹と節の電圧振幅比(腹/節)が2倍

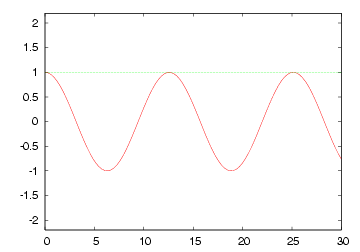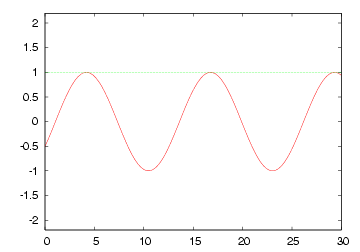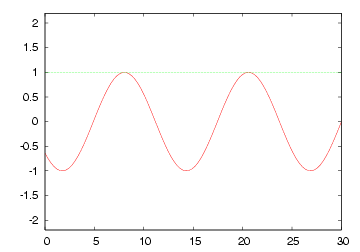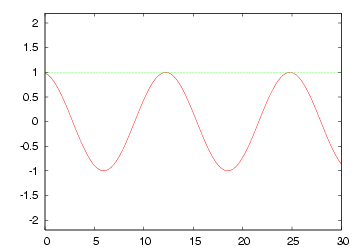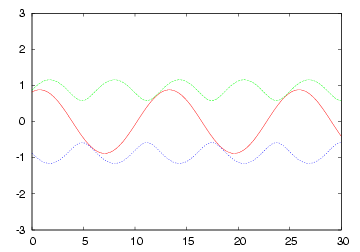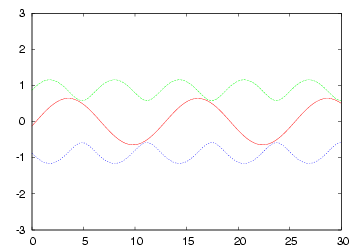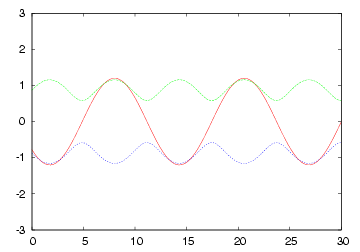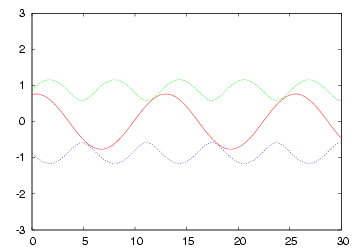
   R= (1/2) * Zo の各部電圧波形	2 * Zo のインピーダンスで終端された場合の 各部電圧波形

3. 電圧定在波比: ρ=∞, 腹と節の電圧比(腹/節)が∞

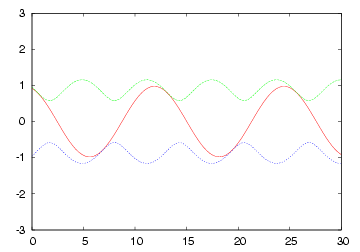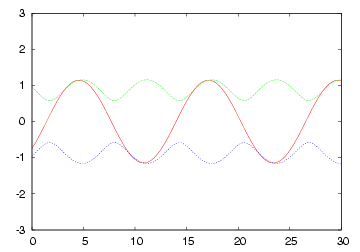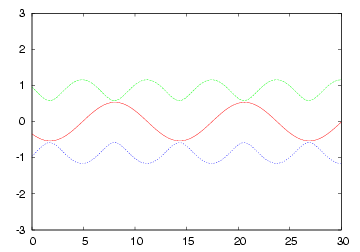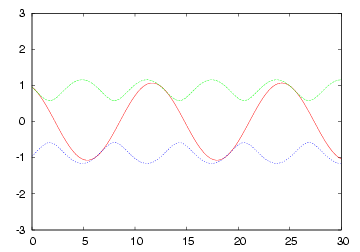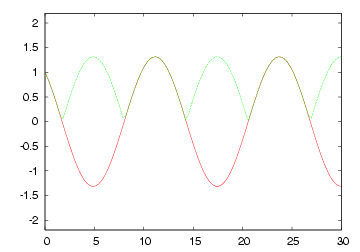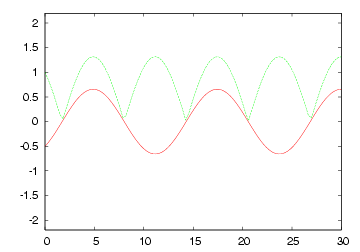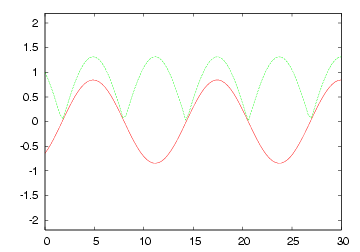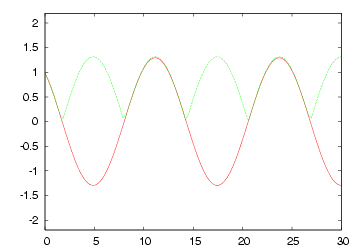
   終端短絡(R=0)の各部電圧波形	終端開放(R=∞)の各部電圧波形

演習の解説